In maths, like life, keeping things simple can really help. When we work with fractions we pretty much always want to simplify them, especially at the end of a problem when we are giving our answer.
We can simplify a fraction when we can divide the numerator and denominator by the same whole number (a common factor), and get whole number (not fraction or decimal) answers.
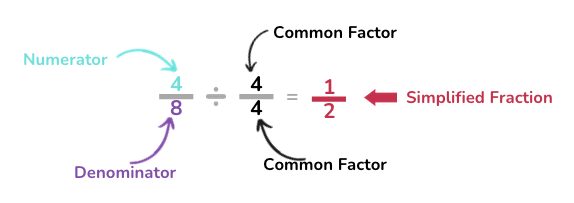
How do we know what to divide by?
There are two methods:
1) We can find the Highest (or Greatest) Common factor.
2) We can find any common factor, and then find another and another until the fraction is in its simplest form.
Either way is fine, but we’re going to use the second method. All you have to do is follow this chart!
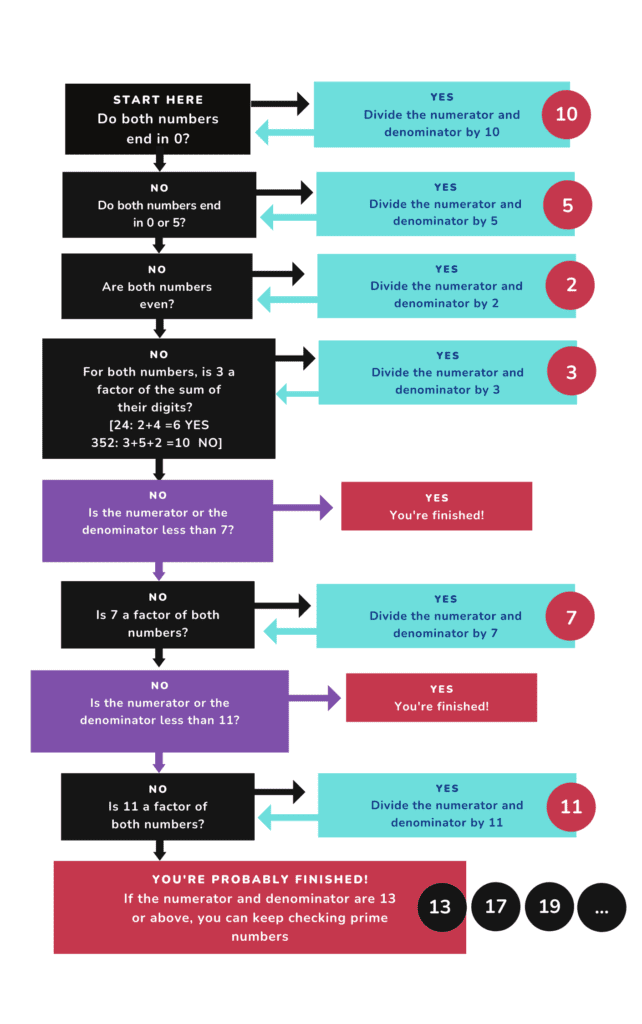
How does this work?
Basically it’s a quick way to check whether the numbers 1 to 12 are common factors.
The easiest numbers to check are 10, 5 and 2 – because we can see immediately if they are factors just by looking at a number – so we start there.
Anything that ends in 0 can be divided by 10
Anything that ends in 0 or 5 can be divided by 5 (picture the 5x table, it contains every number that ends in 0 or 5)
Any even number (ends in 0, 2, 4, 6, or 8) can be divided by 2 (that is actually the definition of an even number)
It makes sense to check the largest number first, so we start with 10. We also need to be aware that any of these numbers could be factors more than once.

Now we’ve checked 10, 5 and 2, what’s next? Let’s look at the numbers 1 to 12 to see what’s left. Obviously 10, 5 and 2 are done, but so is 1 (dividing by 1 doesn’t change a number so it doesn’t matter) and 4, 6, 8 and 12 (we actually checked ALL even numbers when we checked 2). This leaves:
We’ll start with 3. There’s a cool trick for checking if 3 is a factor of a number – you add its digits together, and if that number can be divided by 3 then the whole number can be divided by 3. This works for really big numbers, so feel free to use it as a party trick if you go to those kinds of parties. Why does it work? Check out the explanation here.
Next is 7. There is a trick for this, but it’s a bit complicated. If you don’t know your 7x table you could also use a calculator, long division or count up in 7s.
Then there is 9, but 3 is a factor of 9 so we checked it when we checked 3.
Then we check 11 (it has a complicated trick as well). We’ve now checked all the possible factors up to 12! A lot of the time this will be enough, but a fraction may have bigger common factors. All we have to look at though are PRIME numbers (13, 17, 19, 23…), as every other number is created by multiplying factors we have already checked.
How do we know when we’re finished?
Good question! It can be hard to tell whether a fraction is fully simplified, or you’ve just missed a factor. One way to be sure is when the factor you’re checking is bigger than the numerator or denominator of the fraction. If the numerator is 6, we definitely can’t divide it by 7. So once we get to 3 and we’re checking from the smallest to largest, we can stop when the next factor to check will be bigger than the numerator or denominator.
Have a go yourself!
Just click on the fraction for the answer.
Want your own Simplifying Fractions chart? Download it here!





